همبستگی چیست؟ | بررسی رابطه بین متغیرها در تحلیل دادهها

به گزارش شهر بورس، همبستگی یکی از مفاهیم کلیدی در تحلیل دادهها و آمار است که میزان و نوع ارتباط بین دو متغیر را مشخص میکند. در بسیاری از حوزههای علمی، اقتصادی، اجتماعی و حتی پزشکی، بررسی میزان همبستگی بین متغیرها به تصمیمگیریهای بهتر و دقیقتر کمک میکند. اما آیا همیشه وجود یک همبستگی به معنای یک رابطه علّی است؟ چگونه میتوان این شاخص را اندازهگیری کرد؟ در این مقاله آموزشی، به بررسی دقیق مفهوم همبستگی، روشهای محاسبه آن، تفسیر نتایج و کاربردهای عملی آن خواهیم پرداخت.
همبستگی چیست؟
همبستگی، میزان و جهت رابطه بین دو متغیر را نشان میدهد. اگر تغییر در یک متغیر با تغییر در متغیر دیگر همراه باشد، میتوان گفت که این دو متغیر همبسته هستند. این رابطه میتواند مثبت، منفی یا صفر باشد:

- مثبت: افزایش یک متغیر، با افزایش متغیر دیگر همراه است. (مثلاً افزایش ساعات مطالعه و بهبود نمرات امتحانی)
- منفی: افزایش یک متغیر، با کاهش متغیر دیگر همراه است. (مثلاً افزایش مصرف سیگار و کاهش سلامت جسمی)
- صفر: هیچ رابطه مشخصی بین دو متغیر وجود ندارد.
روشهای محاسبه همبستگی
برای اندازهگیری همبستگی، چندین روش وجود دارد که بسته به نوع دادهها و شرایط، مورد استفاده قرار میگیرند.
۱. ضریب همبستگی پیرسون (Pearson Correlation)
یکی از پرکاربردترین روشهای اندازهگیری همبستگی، ضریب همبستگی پیرسون (𝑟) است که میزان رابطه خطی بین دو متغیر عددی را نشان میدهد. این ضریب مقداری بین -۱ و +۱ دارد:
در این مقاله، به بررسی تفاوتهای اسانس و ادکلن میپردازیم و به شما کمک میکنیم تا تصمیم بگیرید کدام یک برای شما مناسبتر است.
- +۱: همبستگی خطی مثبت کامل
- -۱: همبستگی خطی منفی کامل
- ۰: عدم وجود همبستگی خطی
فرمول ضریب همبستگی پیرسون:
۲. ضریب همبستگی اسپیرمن (Spearman Correlation)
این روش برای دادههای رتبهای (Ordinal) مناسب است و نیازی به فرض توزیع نرمال ندارد. همبستگی اسپیرمن بیشتر در تحلیلهای اجتماعی و روانشناسی استفاده میشود.
۳. ضریب همبستگی کندال (Kendall’s Tau)
این شاخص زمانی به کار میرود که دادهها بهصورت رتبهبندی شده باشند و هدف بررسی میزان توافق بین دو مجموعه رتبه باشد.
تفسیر نتایج
معمولاً مقدار ضریب همبستگی به صورت زیر تفسیر میشود:
| مقدار ضریب همبستگی | تفسیر |
|---|---|
| ۰.۰۰ تا ۰.۱۹ | همبستگی بسیار ضعیف |
| ۰.۲۰ تا ۰.۳۹ | همبستگی ضعیف |
| ۰.۴۰ تا ۰.۶۹ | همبستگی متوسط |
| ۰.۷۰ تا ۰.۸۹ | همبستگی قوی |
| ۰.۹۰ تا ۱.۰۰ | همبستگی بسیار قوی |
نکته مهم: وجود همبستگی به معنای وجود رابطه علّی نیست! ممکن است دو متغیر بهطور تصادفی همبسته باشند یا متغیر سومی وجود داشته باشد که بر هر دو تأثیر میگذارد.
کاربردها
۱. تحلیل اقتصادی و مالی
در بازارهای مالی، بررسی این مفهوم بین داراییهای مختلف به سرمایهگذاران کمک میکند تا سبد سرمایهگذاری خود را بهینه کنند. مثلاً رابطه بین قیمت طلا و ارزش دلار معمولاً منفی است.
۲. تحقیقات پزشکی
در مطالعات پزشکی، بررسی ارتباط بین میزان مصرف دارو و بهبود بیماران میتواند به پزشکان در تصمیمگیری کمک کند.
۳. علوم اجتماعی
در حوزه جامعهشناسی، تحلیل رابطه بین سطح تحصیلات و درآمد میتواند به درک بهتر روندهای اجتماعی کمک کند.
نمودار پراکندگی (Scatter Plot)
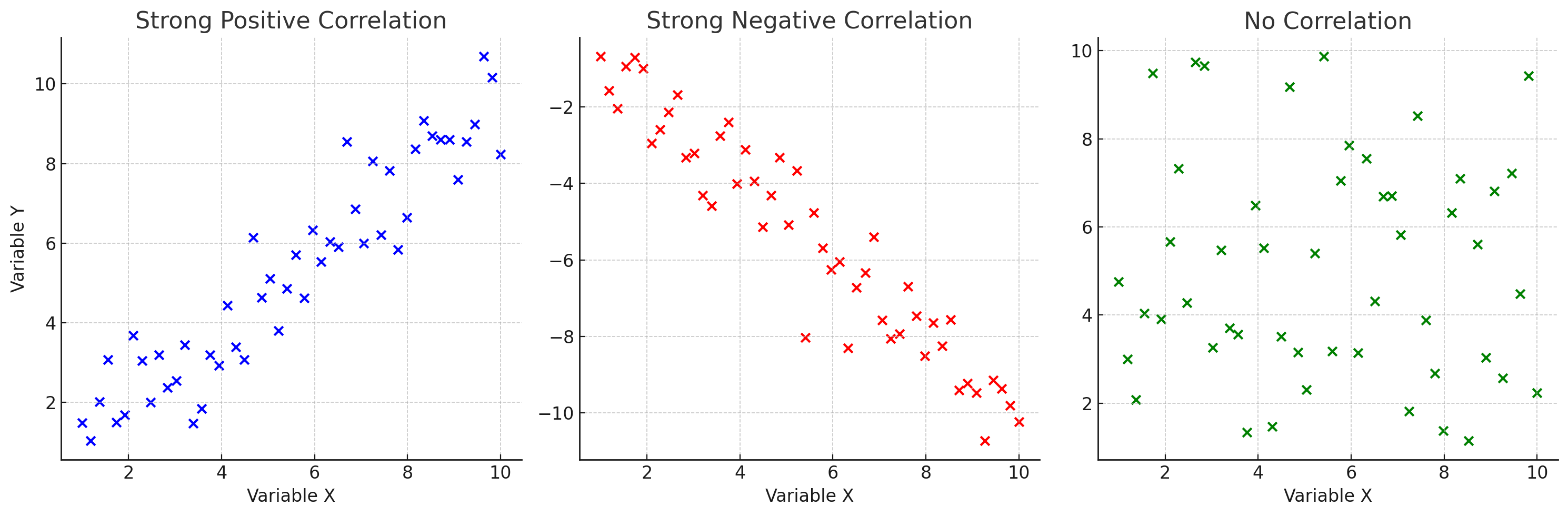
برای نمایش همبستگی بین دو متغیر، نمودار پراکندگی یکی از بهترین روشهاست. در این نمودار، هر نقطه نشاندهنده یک نمونه است و نوع توزیع نقاط نشاندهنده رابطه بین متغیرها خواهد بود.
این نمودار شامل سه بخش مجزا است که هرکدام یکی از انواع همبستگی را نشان میدهد. بررسی این نمودارها به ما کمک میکند تا رابطه بین دو متغیر را بهتر درک کنیم.
۱. همبستگی مثبت قوی (Strong Positive Correlation)
- نقاط داده یک الگوی صعودی را دنبال میکنند.
- بهطور کلی، با افزایش مقدار X، مقدار Y نیز افزایش مییابد.
- ضریب همبستگی مثبت و نزدیک به +1 است.
مفهوم:
- هنگامی که یک متغیر افزایش پیدا میکند، متغیر دیگر نیز تمایل به افزایش دارد.
- این رابطه نشان میدهد که بین این دو متغیر رابطه مستقیم برقرار است.
مثال:
- زمان مطالعه و نمره امتحان: هرچقدر ساعات مطالعه بیشتر باشد، معمولاً نمره بهتری کسب میشود.
- قدرت تبلیغات و میزان فروش: افزایش هزینه تبلیغات معمولاً باعث افزایش فروش میشود.
۲. همبستگی منفی قوی (Strong Negative Correlation)
- نقاط داده یک الگوی نزولی را دنبال میکنند.
- با افزایش مقدار X، مقدار Y کاهش مییابد.
- ضریب همبستگی منفی و نزدیک به -1 است.
مفهوم:
- هنگامی که یک متغیر افزایش پیدا میکند، متغیر دیگر کاهش مییابد.
- این رابطه نشان میدهد که بین این دو متغیر رابطه معکوس برقرار است.
مثال:
- سرعت خودرو و مصرف سوخت: هرچقدر سرعت افزایش یابد، میزان مصرف سوخت (بهینهسازی شده) کاهش پیدا میکند.
- تمرین ورزشی و درصد چربی بدن: افرادی که بیشتر ورزش میکنند، معمولاً درصد چربی بدن پایینتری دارند.
۳. عدم وجود همبستگی (No Correlation)
- نقاط داده بهصورت تصادفی و بدون الگوی مشخص پراکنده شدهاند.
- تغییر مقدار X تأثیر مشخصی بر مقدار Y ندارد.
- ضریب همبستگی نزدیک به 0 است.
مفهوم:
- این وضعیت نشان میدهد که هیچ رابطه معناداری بین دو متغیر وجود ندارد.
- تغییر در یک متغیر باعث تغییر قابل پیشبینی در متغیر دیگر نمیشود.
مثال:
- سایز کفش و میزان هوش: هیچ ارتباطی بین اندازه کفش یک فرد و میزان هوش او وجود ندارد.
- رنگ ماشین و میزان مصرف سوخت: نوع رنگ خودرو تأثیری در میزان مصرف سوخت آن ندارد.
جمعبندی
- همبستگی مثبت نشاندهنده یک رابطه مستقیم است، یعنی هر دو متغیر با هم افزایش یا کاهش مییابند.
- همبستگی منفی نشاندهنده یک رابطه معکوس است، یعنی افزایش یکی منجر به کاهش دیگری میشود.
- عدم وجود همبستگی نشاندهنده عدم ارتباط بین دو متغیر است و تغییر در یکی از آنها تأثیری بر دیگری ندارد.
نکته مهم: همبستگی لزوماً به معنای علیت (Causation) نیست. یعنی فقط به این دلیل که دو متغیر همبسته هستند، نمیتوان نتیجه گرفت که یکی از آنها علت تغییر دیگری است.
کاربرد این مفهوم در تصمیمگیریهای واقعی
- سرمایهگذاری و بازار مالی: تحلیل همبستگی بین داراییهای مختلف به سرمایهگذاران کمک میکند تا بهترین تصمیم را برای تخصیص سرمایه بگیرند.
- پزشکی و سلامت: بررسی همبستگی بین سبک زندگی و بیماریها میتواند به تحقیقات پزشکی کمک کند.
- بازاریابی و فروش: تحلیل ارتباط بین تبلیغات و میزان فروش میتواند در بهینهسازی استراتژیهای بازاریابی مؤثر باشد.
همبستگی یکی از ابزارهای اساسی در تحلیل دادههاست که به پژوهشگران کمک میکند تا روابط بین متغیرها را درک کنند. اما نکته مهم این است که همبستگی لزوماً نشاندهنده رابطه علّی نیست و باید در تحلیلهای علمی از روشهای دقیقتری برای بررسی تأثیرات مستقیم استفاده شود.
برچسب ها :متفرقه
- نظرات ارسال شده توسط شما، پس از تایید توسط مدیران سایت منتشر خواهد شد.
- نظراتی که حاوی تهمت یا افترا باشد منتشر نخواهد شد.
- نظراتی که به غیر از زبان فارسی یا غیر مرتبط با خبر باشد منتشر نخواهد شد.








ارسال نظر شما
مجموع نظرات : 0 در انتظار بررسی : 0 انتشار یافته : 0